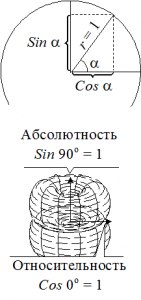
 Тригонометрия — наука о пропорциях треугольников. Поскольку треугольники описывают все физические тела, тригонометрию можно назвать предшевственицей Теории Относительности — «главной науки» о строении Видимой Бесконечности. Но такое суждение несколько лукаво. Суть мироздания можно описать равносторонними треугольниками (см. фильмы про Треугольную Метематику), а тригонометрия исследует закономерности «нарушения равносторонности» — когда гармония соблюдается лишь «отчасти»… Можно сказать, что синус и косинус определяют положение Локального Я на поверхости торойда Души (см. рисунок справа и Вихревую Модель Мира).
Тригонометрия — наука о пропорциях треугольников. Поскольку треугольники описывают все физические тела, тригонометрию можно назвать предшевственицей Теории Относительности — «главной науки» о строении Видимой Бесконечности. Но такое суждение несколько лукаво. Суть мироздания можно описать равносторонними треугольниками (см. фильмы про Треугольную Метематику), а тригонометрия исследует закономерности «нарушения равносторонности» — когда гармония соблюдается лишь «отчасти»… Можно сказать, что синус и косинус определяют положение Локального Я на поверхости торойда Души (см. рисунок справа и Вихревую Модель Мира).
В равносторонних треугольниках всё ясно без математики — там все стороны просто равны. В остальных же треугольниках действует квадратичный закон Пифагора и Косинусов: c^2 = a^2 + b^2 — 2ab Cos C. При C = 0 это уравнение превращается в бином Ньютона для квадрата: (a — b)^2 = a^2 + b^2 — 2ab. Во всех этих уравнениях удивляет их неожиданная сложность. Хоть каждый отрезок представляет собой одномерную величину, но их взаимосвязи описываются квадратами — т.е., для взаимной увязки формальной логики необходимо подняться до 2-мерного восприятия!
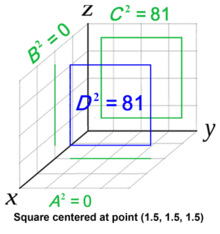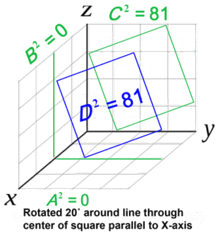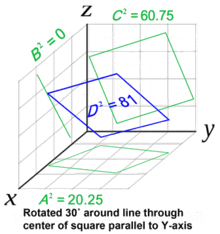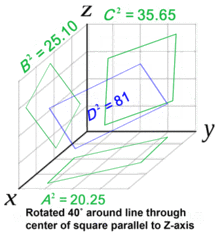
Дальнейшее повышение мерности обьектов не меняет мерности требуемой логики — так как квавдрат площади поверхности равен сумме квадратов площадей проекций на все координатные плоскости: S^2 = S1^2 + S2^2 + S3^2 + … (см. Pythagorean Theorem, Conant-Beyer generalization). То же самое действует и для многомерных обьёмов…
Завораживает также и тот факт, что уравнение a^n + b^n = c^n соблюдается лишь при n = 1 или 2 (Большая Теорема Ферма). Это уравнение привлекло к себе пожалуй самое большое внимание за всю историю цивилизации. При n = 2 оно становится Теоремой Пифагора, получившей наверное самое большое число независимых правильных доказательств, а при n > 2 — Теоремой Ферма, породившей наверное самое больчое число ложных доказательств…
Очевидно, что эти уравнения приблиожают нас к пониманию чего-то очень важного — иначе они не привлекли бы столь великого внимания. Но нащупать суть наверно не удавалось никому — иначе тригонометрия уж давно стала бы наукой о Душе… А попыток совместить эти два понятия было много. Слово Тригонометрия впервые введено Бартоломеем Питискусом, который увлекался также и богословием, и поэтому явно связывал эти два аспекта. Тем же занимались Спиноза и Декарт. Думаю, древние Пифагорийцы тоже видели глубинную суть…
Сегодня нередко тригонометрию преподают как «сборник формул», который нужно просто запомнить. Для этого придумывают разные слоганы и песенки — культивуруют «поверхностное запоминание»… Недавно появилась Рациональная Тригонометрия, в зкоторой обходятся без синусов и косинусов, но глубинная суть тоже не затрагивается. Нужны свежие идеи
Зачем нужны синусы и косинусы?
