 Когда говорим про «математические модели мира», сразу вспоминаются уравнения Максвелла и Шредингера. Но нас интересует собственная модель, основанная на Вихревом Строении Мира (которая описывает не только внешние явления, но и внутренние переживания).
Когда говорим про «математические модели мира», сразу вспоминаются уравнения Максвелла и Шредингера. Но нас интересует собственная модель, основанная на Вихревом Строении Мира (которая описывает не только внешние явления, но и внутренние переживания).
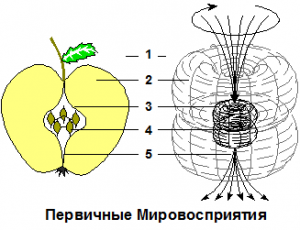
Первый вопрос — как описать вращающийся многослойный вихрь? В разделе Комплексных Чисел показываем, что скорее всего здесь пригодны 8-ми мерные числа (октонионы), но формализм этих описаний столь сложен, что математики даже и не пытаются вникать … даже 4-х мерное описание уравнений Максвелла через кватернионы вызвлало столь много негодований, что математикам срочно потребовалось придумывать новые операторы (векторных производных, роторов, дивергенций), приведших к нынешней векторной алгебре со всеми её проблемами … Поэтому нужно искать какие-то упрощения.
Описание неподвижного вихря достаточно просто — см. Torus meets an equation. А вот описание вращающегося вихря очень даже непросто: Toroidal vortex flow animation
Вихревая структура порождает удивительные математические закономерности, осознать которых я лично пока не способен:
Marko Rodin — Vortex based mathematics
Phi vortex based mathematics torus array
 Иногда вращающийся вихрь заменяют неподвижным ромбическим додекаэдром или просто додекаэдром
Иногда вращающийся вихрь заменяют неподвижным ромбическим додекаэдром или просто додекаэдром
Любая такая модель будет отображать лишь «базовый принцип одного кирпичика» Вселенной. По принципу Голограммы эта модель должна «рекурсивно» распространяться на все части Вселенной — на подобии того, как Мандельброт получил своё множество, бесконечно повторяя одно простое математическое действие.
Так как каждая точка пространства живая и отражает всю целостность Вселенной, то она должна пронизываться собственной воронкой (в случае вихревой модели). Каждая точка должна иметь конечный размер (так как всё одновременно конечно и бесконечно), и этот размер должен быть изменчивым (и у всех точек разным)… Диаметр центральной воронки может быть положительным или отрицательным (в первом случае преобладает разрушительная центробежность, во втором — созидательная центростремительность)
 Иногда голограмную модель заменяют какой-нибудь другой фрактальностью, например — многоуровневым додекаэдром:
Иногда голограмную модель заменяют какой-нибудь другой фрактальностью, например — многоуровневым додекаэдром:
The hyperbolic dodecaverse
… или даже просто встроенными додекаэдрами…
Кепплер построил модель мира, вписывая друг в друга поочерёдно все пять платонических тел…
Цель таких упражнений — развить способность описывать сложные явления простым языком. (Если формальная математика не позволяет чего-то описать достаточно просто, значит нужно изменить математику)
Программа по Мирозданию
Программа по Математике
